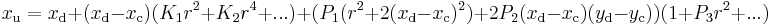Distortion (optics)
| Optical aberration |
|---|
DistortionSpherical aberration |
In geometric optics and cathode ray tube (CRT) displays, distortion is a deviation from rectilinear projection, a projection in which straight lines in a scene remain straight in an image. It is a form of optical aberration.
Contents |
Radial distortion
Although distortion can be irregular or follow many patterns, the most commonly encountered distortions are radially symmetric, or approximately so, arising from the symmetry of a photographic lens. The radial distortion can usually be classified as one of two main types:
- Barrel distortion
- In "barrel distortion", image magnification decreases with distance from the optical axis. The apparent effect is that of an image which has been mapped around a sphere (or barrel). Fisheye lenses, which take hemispherical views, utilize this type of distortion as a way to map an infinitely wide object plane into a finite image area.
- Pincushion distortion
- In "pincushion distortion", image magnification increases with the distance from the optical axis. The visible effect is that lines that do not go through the centre of the image are bowed inwards, towards the centre of the image, like a pincushion. A certain amount of pincushion distortion is often found with visual optical instruments, e.g., binoculars, where it serves to eliminate the globe effect.
A mixture of both types, sometimes referred to as mustache distortion (moustache distortion) or complex distortion, is less common but not rare. It starts out as barrel distortion close to the image center and gradually turns into pincushion distortion towards the image periphery, making horizontal lines in the top half of the frame look like a handlebar mustache.
Mathematically, barrel and pincushion distortion are quadratic, meaning they increase as the square of distance from the center. In mustache distortion the quartic (degree 4) term is significant: in the center, the degree 2 barrel distortion is dominant, while at the edge the degree 4 distortion in the pincushion direction dominates. Other distortions are in principle possible – pincushion in center and barrel at the edge, or higher order distortions (degree 6, degree 8) – but do not generally occur in practical lenses, and higher order distortions are small relative to the main barrel and pincushion effects.
- Occurrence
In photography, distortion is particularly associated with zoom lenses, particularly large-range zooms, but may also be found in prime lenses, and depends on focal distance – for example, the Canon EF 50mm f/1.4 exhibits barrel distortion at extremely short focal distances. Barrel distortion may be found in wide-angle lenses, and is often seen at the wide-angle end of zoom lenses, while telephoto distortion is often seen in older or low-end telephoto lenses. Mustache distortion is observed particularly on the wide end of some zooms, with certain retrofocus lenses, and more recently on large-range zooms such as the Nikon 18–200 mm.
In order to understand these distortions, it should be remembered that these are radial defects; the optical systems in question have rotational symmetry (omitting non-radial defects), so the didactically correct test image would be a set of concentric circles having even separation—like a shooter's target. It will then be observed that these common distortions actually imply a nonlinear radius mapping from the object to the image: What is seemingly pincushion distortion, is actually simply an exaggerated radius mapping for large radii in comparison with small radii. A graph showing radius transformations (from object to image) will be steeper in the upper (rightmost) end. Conversely, barrel distortion is actually a diminished radius mapping for large radii in comparison with small radii. A graph showing radius transformations (from object to image) will be less steep in the upper (rightmost) end.
Chromatic aberration
Radial distortion that depends on wavelength is called "lateral chromatic aberration" – "lateral" because radial, "chromatic" because dependent on color (wavelength). This can cause colored fringes in high-contrast areas in the outer parts of the image. This should not be confused with axial (longitudinal) chromatic aberration, which causes aberrations throughout the field, particularly purple fringing.
Gallery
The names for these distortions come from familiar objects which are visually similar.
Software correction
Radial distortion, whilst primarily dominated by low order radial components,[1] can be corrected using Brown's distortion model.[2] Brown's model caters for both radial distortion and for tangential distortion caused by physical elements in a lens not being perfectly aligned. The latter is thus also known as decentering distortion.
where:
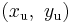 = undistorted image point,
= undistorted image point,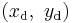 = distorted image point,
= distorted image point,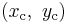 = distortion center (assumed to be the principal point),
= distortion center (assumed to be the principal point),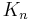 =
= 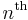 radial distortion coefficient,
radial distortion coefficient,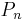 =
= 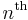 tangential distortion coefficient,
tangential distortion coefficient, =
= 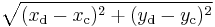 , and
, and = an infinite series.
= an infinite series.
Barrel distortion typically will have a positive term for 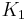 where as pincushion distortion will have a negative value. Moustache distortion will have a non-monotonic radial geometric series where for some
where as pincushion distortion will have a negative value. Moustache distortion will have a non-monotonic radial geometric series where for some  the sequence will change sign.
the sequence will change sign.
Software can correct those distortions by warping the image with a reverse distortion. This involves determining which distorted pixel corresponds to each undistorted pixel, which is non-trivial due to the non-linearity of the distortion equation.[1] Lateral chromatic aberration (purple/green fringing) can be significantly reduced by applying such warping for red, green and blue separately.
An alternative method iteratively computes the undistorted pixel position.[3]
Calibrated
Calibrated systems work from a table of lens/camera transfer functions:
- PTlens is a Photoshop plugin or standalone application which corrects complex distortion. It not only corrects for linear distortion, but also second degree and higher nonlinear components.[4]
- DxO Labs' Optics Pro can correct complex distortion, and takes into account the focus distance.
- The Micro Four Thirds system cameras and lenses perform automatic distortion correction using correction parameters that are stored in each lens's firmware, and are applied automatically by the camera and RAW converter software. The optics of most of these lenses feature substantially more distortion than their counterparts in systems that don't offer such automatic corrections, but the software-corrected final images show noticeably less distortion than competing designs.[5]
Manual
Manual systems allow manual adjustment of distortion parameters:
- Photoshop CS2 and Photoshop Elements (from version 5) include a manual Lens Correction filter for simple (pincushion/barrel) distortion
- Corel Paint Shop Pro Photo include a manual Lens Distortion effect for simple (barrel, fisheye, fisheye spherical and pincushion) distortion.
- The GIMP includes manual lens distortion correction (from version 2.4).
- PhotoPerfect has interactive functions for general pincushion adjustment, and for fringe (adjusting the size of the red, green and blue image parts).
- Hugin can be used to correct distortion, though that is not its primary application.[6]
Related phenomena
Radial distortion is a failure of a lens to be rectilinear: a failure to image lines into lines. If a photograph is not taken straight-on then, even with a perfect rectilinear lens, rectangles will appear as trapezoids: lines are imaged as lines, but the angles between them are not preserved (tilt is not a conformal map). This effect can be controlled by using a perspective control lens, or corrected in post-processing.
Due to perspective, cameras image a cube as a square frustum (a truncated pyramid, with trapezoidal sides)—the far end is smaller than the near end. This creates perspective, and the rate at which this scaling happens (how quickly more distant objects shrink) creates a sense of a scene being deep or shallow. This cannot be changed or corrected by a simple transform of the resulting image, because it requires 3D information, namely the depth of objects in the scene. This effect is known as perspective distortion; the image itself is not distorted, but is perceived as distorted when viewed from a normal viewing distance.
Note that if the center of the image is closer than the edges (for example, a straight-on shot of a face), then barrel distortion and wide-angle distortion (taking the shot from close) both increase the size of the center, while pincushion distortion and telephoto distortion (taking the shot from far) both decrease the size of the center. However, radial distortion bends straight lines (out or in), while perspective distortion does not bend lines, and these are distinct phenomena. Fisheye lenses are wide-angle lenses with heavy barrel distortion and thus exhibit both these phenomena, so objects in the center of the image (if shot from a short distance) are particularly enlarged: even if the barrel distortion is corrected, the resulting image is still from a wide-angle lens, and will still have a wide-angle perspective.
See also
- Anamorphosis
- Angle of view
- Cylindrical perspective
- Distortion
- Texture gradient
- Underwater vision
- Vignetting
References
- ^ a b de Villiers, J. P.; Leuschner, F.W.; Geldenhuys, R. (17–19 November 2008). "Centi-pixel accurate real-time inverse distortion correction". 2008 International Symposium on Optomechatronic Technologies. SPIE. http://spie.org/x648.html?product_id=804771.
- ^ Brown DC (1966). "Decentering distortion of lenses.". Photogrammetric Engineering. 7: 444–462.
- ^ "A Four-step Camera Calibration Procedure with Implicit Image Correction". http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=609468. Retrieved 19 January 2011.
- ^ "PTlens". http://epaperpress.com/ptlens/. Retrieved Jan. 2, 2012.
- ^ http://www.dpreview.com/articles/distortion/
- ^ "Hugin tutorial – Simulating an architectural projection". http://hugin.sourceforge.net/tutorials/architectural/en.shtml. Retrieved 9 September 2009.
- ^ "Adaptive Optics". Technology for Telescopes. ESO. http://www.eso.org/public/teles-instr/technology/adaptive_optics.html. Retrieved 2 November 2011.
- Paul van Walree. "Distortion". Photographic optics. http://toothwalker.org/optics/distortion.html. Retrieved 2 February 2009.
- Jason de Villiers. "Centi-pixel accurate real-time inverse distortion correction". Photogrammetry. http://sites.google.com/site/jasondevilliers/home/research/Hyp2paper29May2008.pdf?attredirects=0. Retrieved 9 September 2009.
External links
- Lens distortion estimation and correction with source code and online demonstration